Ejercicio 3
Expresión binaria de un número natural
Un método rápido para expresar un número natural en sistema de numeración en base 2 es el ir dividiendo el número y los sucesivos restos entre potencias de 2, tomando nota de los cocientes resultantes. Por ejemplo:
78 en base 2: |
|
78 entre 64 da 1 |
Resto 14 |
14 entre 32 da 0 |
Resto 14 |
14 entre 16 da 0 |
Resto 14 |
14 entre 8 da 1 |
Resto 6 |
6 entre 4 da 1 |
Resto 2 |
2 entre 2 da 1 |
Resto 0 |
0 entre 1 da 0 |
Resto 0 |
La expresión binaria de 78 estará formada por los cocientes: 1001110
El ejercicio que se propone consiste en implementar este algoritmo en una hoja de cálculo.
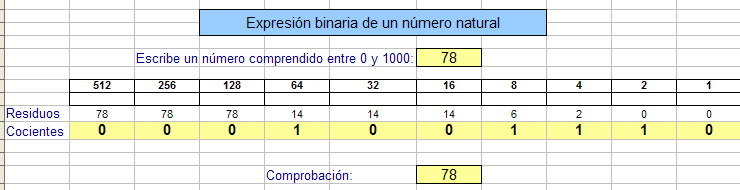
En la imagen figuran todas las potencias de 2 entre 1 y 512, para que el algoritmo se pueda aplicar a todos los números naturales menores que 1000. Puedes ampliar a más potencias si lo deseas.
La fila de residuos se consigue con la función RESIDUO(A;B). El primero se consigue comparando el número dado con 512, el segundo se calcula igual, pero a partir del primer resto, que en la imagen vuelve a ser 78, y así se siguen alculando unos residuos a partir de otros.
La fila de cocientes se forma a partir de la función COCIENTE(a;b), dividiendo cada residuo anterior entre la correspondiente potencia.
La comprobación la consigues mediante la función SUMAPRODUCTO aplicada a las potencias y los cocientes. Si no lo logras así, búscate otro método similar.