Ejercicio 2
Búsqueda de valor destino en la Enseñanza de las Ciencias
Todas las materias de Ciencias presentan ecuaciones que no se pueden resolver mediante métodos elementales. El segundo ejercicio que te proponemos consiste en resolver dos de estas ecuaciones imposibles de abordar en la enseñanza no universitaria, en concreto las referentes al perímetro y la superficie de un segmento circular.
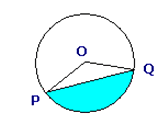
En efecto, si llamamos A al ángulo POQ del segmento circular y R al radio OP, tanto el área AR como el perímetro P presentan unas fórmulas en las que es imposible despejar el ángulo A
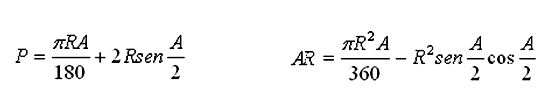
La fórmula del área sólo es válida si el ángulo es inferior a 180º. En caso contrario habría que cambiar el signo - por el +
Construye un modelo inspirándote en ecuacion2.ods, pero con dos estructuras distintas de búsqueda de valor destino, y resuelve con él estas dos cuestiones:
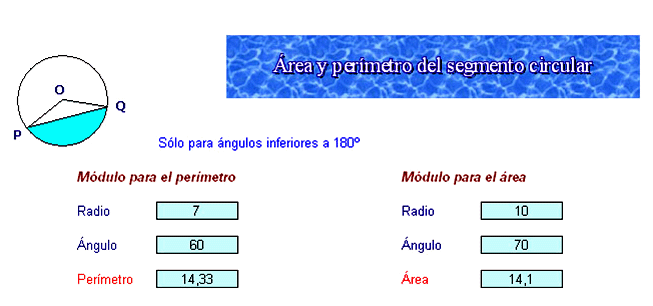
(A) ¿Qué ángulo ha de tener un segmento circular de radio 7 cm y de perímetro 17,6 cm?
(B) ¿Qué ángulo debería tener otro de radio 10 para que su área fuera de 11,8 cm2?
Tu modelo debe contener los elementos que puedes observar en la figura
La imagen del segmento circular la puedes incluir desde este mismo documento con Copiar y Pegar.
El cuadro de texto del título puedes cambiarlo a tu gusto.
Las dos fórmulas de arriba deberán estar contenidas en las celdas de perímetro y área, y referida cada una al radio y ángulo que figura sobre ella, para que constituyan módulos independientes. Observa que los valores están cercanos a los que te piden las cuestiones.
Vas a tener una dificultad, y es que las funciones SENO y COS sólo actúan sobre radianes en esta hoja de cálculo, por lo que tendrás que escribirlas así:
SENO(RADIANES("Celda del ángulo"/2)) y COS(RADIANES("Celda del ángulo"/2))
Sustituye la expresión "Celda del ángulo" por las referencias concretas de las celdas que lo contienen. Las soluciones exactas que te deben dar son : (A) 74,61º (B) 65,77º.