Buscar un valor destino
Una ayuda importante para la resolución de problemas es la posibilidad de las Hojas de Cálculo de despejar una variable en una fórmula. Suele llamarse persecución de objetivos o búsqueda de valor destino. Consiste en ajustar el valor de una celda para conseguir otro valor determinado en otra celda distinta.
Abre el modelo ecuacion2.ods, que contiene una estructura más sencilla que el anterior y resuelve ecuaciones de cualquier tipo, no necesariamente de primer grado.
Su valor educativo no es muy grande, ya que la potencia de cálculo que contiene produce más admiración que motivación por entender el algoritmo implementado. No obstante, se puede usar para comprobar soluciones ya encontradas o para resolver ecuaciones inabordables por otros métodos.
La resolución se basa en la herramienta Buscar valor destino
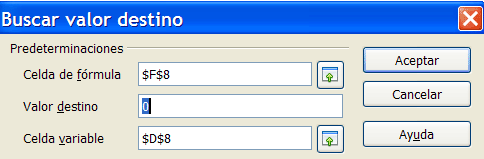
Esta herramienta necesita tres datos (dos celdas y un valor):
a) Celda de la fórmula: Es una celda que contiene una fórmula cuyo valor al evaluarla queremos fijar. En este modelo se trataría de la celda F8, que, como verás, contiene la ecuación.
b) Valor destino: Es el valor que deseamos que contenga la celda de la fórmula. En este caso debemos lograr que valga cero.
c) Celda variable: Contiene un valor del cual depende el resultado de la celda de la fórmula. Este valor es el que deseamos que el ordenador calcule a fin de que aparezca en la celda variable el valor deseado. En este caso se tratará del valor de X, contenido en la celda D8, y por tanto la solución de la ecuación.
Esto, en lenguaje algebraico, equivale a despejar una variable en una fórmula.
Al abrir el modelo la celda F8 contiene la fórmula =X^2+X-200, que se corresponde con la resolución de la ecuación de segundo grado x2 + x – 200 = 0. Esta celda será la celda de fórmula y su valor destino será cero. La celda D8 contiene el valor de x, luego será la celda variable.
Podemos plantearnos cualquier otra ecuación. Por ejemplo, deseamos saber en qué instante un cuerpo arrojado hacia arriba verticalmente, con ecuación de movimiento 20t-4,9t2 alcanza una determinada altura, por ejemplo 15 m. Sabemos que este problema puede tener dos soluciones, una, o ninguna. Con este procedimiento sólo encontramos una, la que esté más al alcance del valor previo que escribamos.
La resolución se consigue con las siguientes operaciones:
- Escribe en la celda de X un valor cualquiera que produzca un resultado no muy grande en el valor de la ecuación. Podíamos escribir 2 segundos. Escribe la fórmula =20*X-4,9*X^2-15 en la celda F8, que según el planteamiento del problema, debe ser igual a cero.
- Activa la orden Herramientas > Búsqueda de valor destino...
- Como celda de fórmula escribe F8
- Como valor destino escribe un CERO
- En celda variable escribe D8
- Pulsa Aceptar y se ajustará el valor de la celda variable a la solución de la ecuación. Se tardan 0,9902 segundos en alcanzar la altura de 15 metros.
Repite el cálculo, pero escribiendo 5 segundos en la celda D8 ¿qué ocurre? ¿qué significado físico tiene esta otra solución?
Cambia ahora los 15 metros que has escrito en la fórmula de la celda F8 por 40 metros. ¿Qué ocurre entonces? ¿Qué significa el valor de 2,05 s. propuesto?
Como ves, es una herramienta muy útil y fácil de manejar, y que esconde más potencia de cálculo de la que parece en un primer estudio.
Esta técnica la puedes usar en cualquier cálculo de las materias de Ciencias, siempre que desees despejar una variable de una fórmula. Además admite toda clase de funciones matemáticas en su resolución, permitiendo resolver ecuaciones del tipo XcosX = 0,3 ó X + LN(X) = 4. En estos casos debes respetar la forma de escribir las funciones en OpenOffice.org Calc.
