 |
► FAQ (Respuestas a preguntas frecuentes)
► Procedimientos
¿Cómo se instala GeoGebra?
Ver las instrucciones en el apartado Instalación del Módulo 1.
No puedo borrar un objeto, ¿por qué?
Podemos otorgar a cualquier objeto la propiedad de fijo. Un objeto fijo no se puede mover, incluso aunque sea libre o semilibre. Tampoco se puede modificar, redefinir o eliminar, al menos hasta que no se modifique esa propiedad.
¿Se pueden omitir los espacios en las expresiones algebraicas?
En la expresión "b x", no hay que omitir el espacio entre "b" y "x" el espacio es el operador de multiplicación (equivale a *). Si se omite, GeoGebra consideraría "bx" como variable no definida. Por otra parte, si en vez del parámetro b colocamos números concretos (p.e., 3x) podríamos omitir el operador multiplicación, pues GeoGebra sólo puede interpretar "3x" como un producto, nunca como el nombre de un objeto (los nombres siempre comienzan con una letra). Naturalmente, si escribimos "x3" se vuelve a interpretar como variable, no como producto.
En cualquier otro caso, es decir, cuando el espacio no puede ser interpretado como el operador multiplicación (por ejemplo, porque ya hay un operador), los espacios no se consideran. Así, es equivalente introducir " 3 + 7 " que "3+7", o bien, "3 7" que "3 7" (producto de 3 por 7).
¿Cómo se pone una construcción en una página web?
En el apartado Archivo de la sección Menús de la Ayuda se ofrecen los detalles.
¿Se pueden mostrar y después ocultar pasos de la construcción?
Sí, gracias al comando PasoConstrucción. Con su ayuda, al usar la Barra de Navegación podemos ir mostrando temporalmente algunos procedimientos particulares de la construcción, hasta determinado paso, y a partir de él ocultarlos. En el apartado El tesoro del módulo 4 se muestra un ejemplo.
¿Se puede impedir el escalado de los objetos?
Sí, gracias al comando Esquina. Las siguientes construcciones sirven de ejemplo de uso:
|
|
|
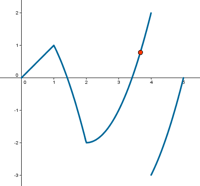
¿Se pueden representar funciones a trozos?
Sí, puede usarse el comando booleano Si para crear una función definida a trozos.
Ejemplos:
- Si [x < 1, x + 3, x - 1]
- Si [x < 1, Función[x + 4, -10, 1], x - 1]
Pueden usarse derivadas e integrales de tales funciones e intersecarlas como funciones “normales”.
Si los trozos son muchos, el procedimiento anterior ocasiona la aparición de condicionales anidados (comandos Si dentro de otros comandos Si, etc.). En tal caso, puede ser conveniente usar una función auxiliar para ayudarnos a separar los trozos, como se muestra en el siguiente ejemplo correspondiente a una función f(x) que toma diferentes expresiones f1(x), f2(x), f3(x) y f4(x) en los intervalos [0,1), [1,2), [2,4) y [4,5], respectivamente:
z = Si[x < 0 || x > 1, 0, 1]
f = Función[z(x) f_1(x) + z(x - 1) f_2(x) + z((x - 2) / 2) f_3(x) + z(x - 4) f_4(x), 0, 5]
Clic en esta imagen abre la
construcción de GeoGebra
¿Dispone GeoGebra de la función Parte Entera?
No, pero se puede construir fácilmente a partir del operador "floor" (entero igual o menor que el número dado), usando el procedimiento para representar funciones a trozos:
parteEntera = Si[x<0, floor(x+1), floor(x)]
¿Puede impedirse el desplazamiento de un objeto basado en puntos libres?
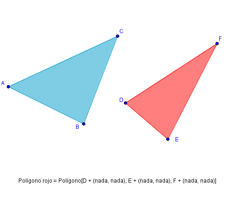
Sí, añadiendo a esos puntos libres, al definir el objeto, una variable nula. Ver el siguiente ejemplo. El polígono azul se puede arrastrar con el ratón, al contrario que el polígono rojo.
Clic en esta imagen abre la
construcción de GeoGebra
¿Se pueden poner parámetros como límites de un deslizador?
Directamente, no se puede. Pero sí se puede simularlo, con un pequeño truco. La clave está en crear un deslizador entre 0 y 1 y después variar algebraicamente este intervalo [0, 1].
En la siguiente construcción tenemos un deslizador h0 que varía entre 0 y 1. A partir de él, creamos el parámetro h que variará en [a, b]:
h = a + (b - a) h0
Clic en esta imagen abre la
construcción de GeoGebra
Ahora basta hacer depender los objetos de h en vez de h0.
Además de h = a + (b - a) h0, que varía siempre entre a y b, otras posibilidades son:
- h = Mínimo[a, b] + (Máximo[a, b] - Mínimo[a, b]) h0
que varía entre a y b cuando a es menor o igual que b; si a es mayor que b, varía entre b y a.
- h = Mínimo[b, a + (b - a) h0]
que varía entre a y b cuando a es menor o igual que b. Si a es mayor que b, queda fijo en b.
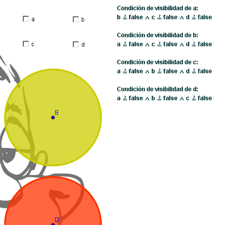
¿Se pueden crear casillas de control de elección excluyente?
Directamente, no se puede. Pero sí se puede simularlo, con un pequeño truco. La clave está ocultar todas las casillas salvo la elegida en cuanto se elija una, y volver a mostrar todas las elecciones posibles al destildarla. En el siguiente ejemplo se detalla el procedimiento.
Clic en esta imagen abre la
construcción de GeoGebra
¿Puede limitarse la libertad de un punto a un área?
Normalmente, no. Pero existe alguna excepción. Observemos la siguiente construcción:
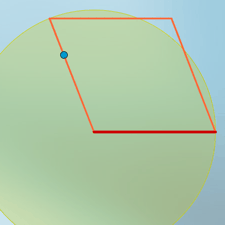
Clic en esta imagen abre la
construcción de GeoGebra
Si el punto azul descansa sobre el segmento, ¿cómo es posible que dirija su movimiento?
El truco reside en que el punto azul no descansa sobre el segmento, sino que es
éste el que se construye a partir de aquél. El deslizador r varía entre 0 y 1.5,
el deslizador 
entre 0 y 360º. Un punto definido directamente como:
(r;
)
aún siendo
dependiente, tendrá libertad de movimientos en los límites que permita r y
. Esto significa
que el punto así definido estará restringido al sector circular centrado en el
origen de coordenadas, de radio r y ángulo los límites de
.
En el modelo titulado "Tangencial" del apartado "Otros modelos" del módulo 4 (Construcciones vs. dibujos) podemos ver un ejemplo de este uso.
Existe otra excepción, que se expone en la siguiente construcción:
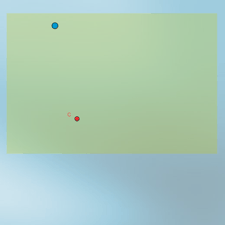
Clic en esta imagen abre la
construcción de GeoGebra
Ahora hay dos parámetros a y b, con límites en [a1, a2] y [b1, b2], respectivamente. El punto azul está definido como:
(a+x(C), b+y(C))
donde C es otro punto cualquiera.
Un punto definido directamente de esta forma, aún siendo dependiente, tendrá libertad de movimientos en los límites que permita a y b. Esto significa que el punto así definido estará restringido al rectángulo con vértices opuestos en C + (a1,b1) y C + (a2,b2).
¿Por qué la definición de una recta afecta a paralelas y perpendiculares?
En los siguientes ejemplos se detalla la causa.
|
Clic en esta imagen |
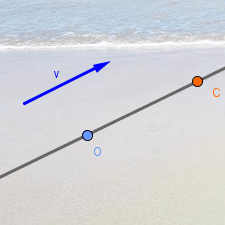
Una recta definida por un punto O y un vector
v tiene por ecuación vectorial:
X = O + λ v
Al colocar un punto C en esa recta, GeoGebra le asigna un valor λC del parámetro λ.
Si variamos el módulo de v, el parámetro λC se mantiene constante, por lo que varía la posición absoluta de C. Es decir, GeoGebra toma el módulo del vector director v como “vector base” de la recta. |
|
Clic en esta imagen |
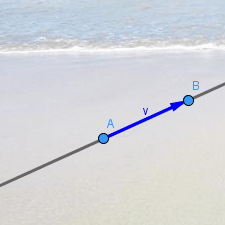
Una recta definida por dos puntos A y B
equivale a estar definida por el punto A y el vector v = AB. Ecuación
vectorial:
X = A + λ v
Al colocar un punto C en esa recta, GeoGebra le asigna un valor λC del parámetro λ.
Si variamos la posición de B, el parámetro λC se mantiene constante, por lo que varía la posición de C. |
|
Clic en esta imagen |
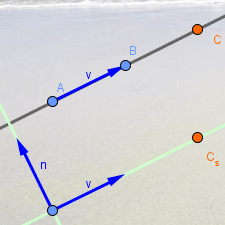
GeoGebra usa el vector director v de la recta
para establecer el vector director de cualquier recta paralela (v) y el
vector director de cualquier recta perpendicular (n, normal a v).
Así que al variar el módulo de v (por ejemplo, desplazando B) todos los puntos de las tres rectas (r, s y t) se desplazan, ya que la posición de todos esos puntos depende de A y B. |
