Objetivos

Las fotografías suelen presentar problemas de exactitud al trabajar directamente sobre ellas. El punto de vista, la perspectiva, la óptica, el desvío de la frontal o del cenit... son características que perjudican seriamente una medición precisa. Sin embargo, resultan excelentes puentes entre la realidad y la abstracción. Un boceto de unos cuantos segmentos y arcos realizado sobre el papel en blanco carece, para mucha gente, del atractivo que aporta una fotografía concreta (seguramente más de un matemático opinará lo contrario, pero es porque ya está habituado a apreciar la belleza de las formas abstractas, algo poco habitual entre los alumnos).

En este ejemplo hemos elegido la foto de un faro. La usaremos para comprobar que con un medidor de ángulos y un poco de trigonometría (teorema del seno) podemos calcular fácilmente la altura del faro.

Herramientas y comandos

Usaremos los comandos Segmento y Semirrecta, junto con las siguientes herramientas.

	Punto		Intersección		Centro
	Segmento		Ángulo		Texto
	Imagen

 Los objetos creados por las herramientas con fondo verde son desplazables (a no ser que su definición se base en puntos que no sean libres).

Construcción paso a paso

 Antes de empezar, puede ser buena idea echar un vistazo al "Ejemplo de construcción" que se encuentra en esta página. Incluso podemos ayudarnos de la Barra de Navegación para realizar un rápido recorrido por los pasos.

Primero prepararemos el escenario.

Preparación Sí No Automático Guardar la siguiente imagen en el disco duro (clic derecho sobre la imagen y elegir "Guardar imagen como..."): (de Wikimedia, foto de JeremyA, distribución libre con licencia CC shareAlike)

Insertaremos a continuación la imagen guardada del faro.

Etapa 1 Clic sobre el botón correspondiente a la herramienta  Imagen. Clic sobre la Vista Gráfica (también se podría hacer clic sobre un punto creado previamente). La posición (o el punto ya creado) sobre la que hace clic se convertirá en la esquina inferior izquierda de la imagen.

Aparece un cuadro de diálogo para visualizar archivos.

Etapa 2 Buscar y seleccionar la imagen del mapa (faro.jpg) que hemos guardado previamente. Elegir Elige-y-Mueve (o pulsa Esc). Arrastrar la imagen hasta la posición que deseemos. Abrir el menú contextual de la imagen (clic derecho sobre ella). En el cuadro de diálogo Propiedades, pestaña Estilo, establecer el sombreado en el 50%.

El faro mide unos 32 metros de altura. Preparamos la escala para que se ajuste aproximadamente a ese dato, haciendo zoom. Centramos la imagen de forma que el origen de coordenadas se sitúe en la base del faro. Para que la imagen no ralentice el funcionamiento de GeoGebra, la convertimos en fondo. Esto hará que no responda al clic derecho, por lo que si posteriormente deseamos modificar alguna propiedad de ella o borrarla, tendremos que buscarla abriendo la ventana de propiedades de un objeto cualquiera o en el Protocolo de la Construcción.

Etapa 3 Abrir el menú contextual de la imagen (clic derecho sobre ella). En el cuadro de diálogo Propiedades, pestaña Básico, activar la casilla Imagen de Fondo.

Abrir el archivo de GeoGebra que aparece en el Ejemplo de Construcción.

Etapa 4 Con ayuda del Protocolo de la Construcción y de la Barra de Navegación, analizar el proceso de construcción e intentar reproducirlo.

Ejemplo de construcción

El faro

Clic en esta imagen abre la construcción de GeoGebra

Propuesta de construcción

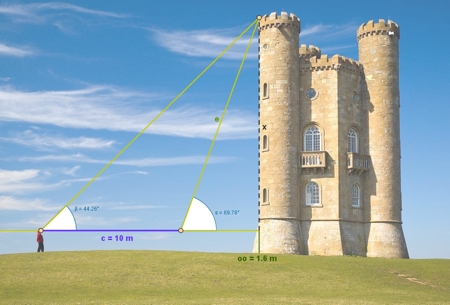
Realizar una construcción similar a la de la imagen anterior con la siguiente imagen (clic derecho sobre la imagen y elegir "Guardar imagen como..."). Considerar que la altura de los ojos de la persona continúa siendo 1.6 m.   (de Wikimedia, foto de Newton2, distribución libre con licencia CC shareAlike)   El resultado puede ser semejante al que muestra la siguiente imagen (la altura real de la torre es de unos 17 m).

Comentarios

Hemos añadido a la construcción de ejemplo otro procedimiento de cálculo, suponiendo que el faro no tuviese grosor. Podemos comprobar que el error cometido es considerable. También podemos aprovechar este cálculo para hallar el radio de la base del faro.

De manera similar, se pueden realizar otras construcciones basadas en la semejanza de triángulos o en procedimientos trigonométricos. Algunas de estas situaciones, muy conocidas, se exponen a continuación como propuestas de construcción.

 Investigación:

• Nos encontramos en la costa justo frente a un barco y deseamos saber a qué distancia se encuentra de nosotros. Nos movemos hacia un lado en línea recta unos cuantos pasos. Dejamos una señal (una piedra, por ejemplo) y seguimos andando, recorriendo la misma distancia de nuevo, de forma que la señal quede justo a mitad del trayecto. Después, giramos 90º hacia el interior y contamos los pasos hasta que vemos la señal alineada con el barco. El número de pasos contados nos dará la distancia que deseábamos conocer.
• Vemos una torre al otro lado de un río y queremos saber la distancia que nos separa de ella. Colocamos dos señales a nuestro lado del río, separadas unos cuantos pasos, que medimos. Desde cada una, medimos el ángulo que forma la torre con la otra señal. Con esta información, una distancia y dos ángulos, podemos averiguar la distancia desde cualquiera de las señales a la torre.
• Vemos dos torres al otro lado de un río y queremos saber la distancia que las separa. Colocamos dos señales a nuestro lado del río, separadas unos cuantos pasos, que medimos. Desde cada una, medimos el ángulo que forma cada torre con la otra señal y las dos torres entre sí. Con esta información, una distancia y cuatro ángulos, podemos averiguar la distancia entre las torres.