Objetivos

Usaremos GeoGebra para crear rápidamente figuras poligonales con vértices en la cuadrícula. El área de cada una de estas figuras es sencilla de calcular simplemente contando cuántas casillas o fracciones de casillas abarca. No hace falta recurrir a ninguna fórmula, así que es una buena actividad para profundizar en los conceptos de área, perímetro y unidades. Encontraremos que el cálculo del perímetro no resulta tan evidente (este hecho puede servir de estímulo para introducir la importancia del teorema de Pitágoras).

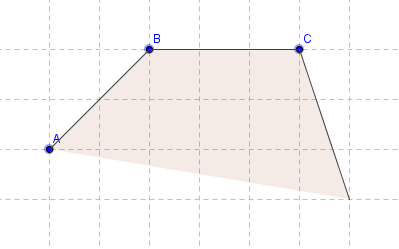
Por otra parte, es habitual la confusión numérica entre número de "puntos de la cuadrícula" (podemos llamarlos nodos, marcas, cruces, vértices, intersecciones...) y número de segmentos unidad. Por ejemplo, en la siguiente imagen se aprecia que la separación entre los 4 puntos no es de 4 unidades lineales, sino sólo 3:

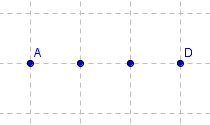
Se podrán redistribuir los vértices del polígono, así como crear nuevos polígonos.

 Esta actividad es muy flexible en cuanto a la forma de la figura o figuras creadas, por lo que puede ser aprovechada para impulsar la imaginación y creatividad de los alumnos.

Herramientas y comandos

Sólo precisaremos de dos herramientas: la herramienta fundamental para mover y seleccionar (herramienta  Elige-y-Mueve) y la herramienta  Polígono. Las herramientas que se encuentran con fondo verde indican que son creadores de objetos desplazables, al menos mientras no se fije alguno de sus elementos.

Elige-y-Mueve

Polígono

 La herramienta fundamental (Elige-y-Mueve) la daremos por supuesta en lo sucesivo.

Una vez dibujado un polígono, procederemos a variar su "estilo" (grosor de los segmentos, colores, transparencia...) a nuestro gusto.

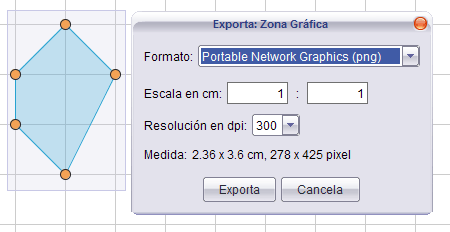
Al tratarse de la primera actividad, practicaremos también los procedimientos para guardar archivos y exportar imágenes, descritos en el apartado Menús de la sección Ayuda.

 Los botones Deshace y Rehace son muy útiles para devolver la construcción a un estado anterior.

Construcción paso a paso

Primero prepararemos el escenario.

Preparación No Sí Activa (Cuadrícula)

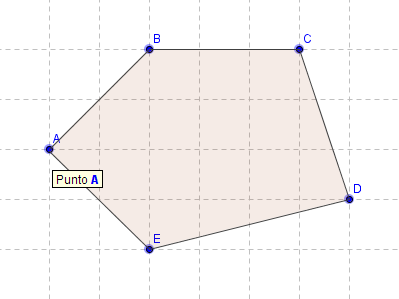
Dibujaremos un pentágono (para cualquier otro polígono se procede de forma similar).

Etapa 1 Clic sobre el botón correspondiente a la herramienta Polígono. Marcar (clic sobre él) un punto de la cuadrícula. Quedará rotulado automáticamente con la letra A.

 Observemos que en la Vista Algebraica apareció también el punto A con sus coordenadas.

Etapa 2 Marcar otros dos puntos distintos de la cuadrícula. Terminar de marcar la serie de cinco puntos, y por último volver a marcar el primer punto A. Seleccionar la herramienta Elige-y-Mueve (o pulsar la tecla Esc). Probar a mover el polígono con ayuda de esta herramienta. Clic derecho sobre el polígono, sus vértices y sus lados para variar las propiedades de estilo a gusto.

 Podemos hacer clic sobre el objeto en la Vista Gráfica o en la Vista Algebraica. A veces, debido a la cercanía de los objetos geométricos, resulta más cómodo emplear la Vista Algebraica.

Etapa 3 Averiguar el área del polígono construido, sirviéndonos de la cuadrícula. ¿Podemos averiguar de igual forma el perímetro, sin recurrir a fórmula o resultado alguno? Enmarcar la figura arrastrando el ratón y exportar el cuadro enmarcado como imagen "png" usando el menú Archivo > Exporta. Guardar el archivo usando el menú Archivo > Guarda. Mover los puntos hasta formar un rectángulo. ¿Se puede ahora averiguar el perímetro con sólo la ayuda de la cuadrícula? ¿En todos los casos?

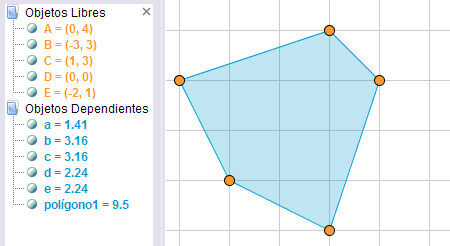
Ejemplo de construcción

Pentágono

Clic en esta imagen abre la construcción de GeoGebra

Propuesta de construcción

Realizar una construcción similar que muestre un recinto heptagonal. Deben verse los rótulos de los vértices, pero no los rótulos de los lados ni el rótulo del polígono. Escribir el enunciado de un problema basado en la figura construida.

Comentarios

Existen diversos procedimientos para contar las casillas o fracciones de casillas correspondientes al área de la figura. Algunos emplean la disección y adición, cortando y sumando las partes simples resultantes. Otros emplean la sustracción, restando el área de aquellas partes que faltan para obtener un rectángulo.

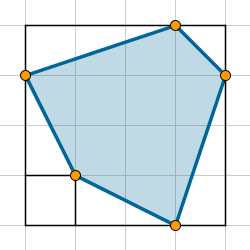
Merece la pena dedicar tiempo a discutir la eficacia de estos métodos y sus variantes sobre diversas figuras. Un método puede ser muy rápido sobre alguna figura, pero volverse relativamente lento sobre otras. Esto es muy habitual en Matemáticas, de ahí la conveniencia de disponer siempre de varios métodos o formas de enfocar el problema.

A los pocos ensayos, los alumnos se darán cuenta de que el área que buscan aparece en la Vista Algebraica como valor del polígono. Si se quiere impedir esto, basta ocultar la Vista Algebraica en el applet.

También se puede formular el problema a la inversa: prefijar el valor (entero o mitad de entero) de un área y solicitar el correspondiente ejemplo de polígono (uno cualquiera o con un número prefijado de lados o con alguna propiedad como cierta simetría...).

 Investigación:

• Valorar la dificultad del siguiente problema: "Encontrar todos los triángulos de área 1 construibles sobre una cuadrícula de 3x3 unidades." ¿Es tan fácil como parece? ¿Tiene la misma dificultad resolverlo en papel que con GeoGebra?
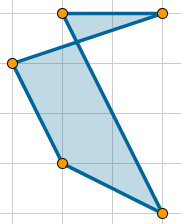
• ¿Qué sucede con los polígonos cruzados (los no simples, aquellos en los que al menos dos lados se intersecan)? ¿Continúa siendo sencillo el cálculo del área? ¿El valor que GeoGebra otorga al polígono sigue correspondiendo al área?
• Problema lógico: Demostrar que cualquier pentágono como estos (con sus cinco vértices en las intersecciones de la cuadrícula, sin que haya tres alineados) siempre tendrá alguno de sus lados o diagonales pasando exactamente por otra intersección. (Indicación: observar los 4 casos posibles de paridad de las coordenadas en los 5 vértices.)